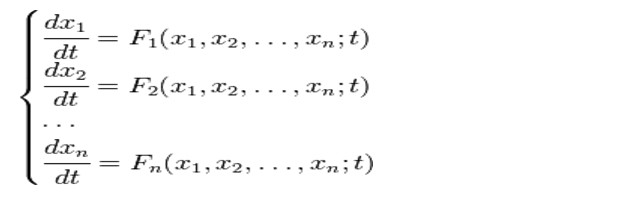Примери за системи от линейни уравнения: метод за решаване

Системите от уравнения са широко използвани викономическо математическо моделиране на различни процеси. Например при решаване на управленски задачи и планиране на производството, логистични маршрути (транспортна задача) или поставяне на оборудване.

Уравняващите системи се използват не само в областта на математиката, но и във физиката, химията и биологията, при решаването на проблемите при намирането на размера на населението.

Система от линейни уравнения се нарича две или повечеУравнения с няколко променливи, за които е необходимо да се намери общо решение. Такава последователност от числа, за която всички уравнения се превръщат в истински равенства или доказват, че последователността не съществува.

Линейното уравнение

Уравненията на формата ax + by = c се наричат ​​линейни. Нотата x, y е неизвестна, стойността на която трябва да се намери, b, a са коефициентите на променливите, c е свободният термин на уравнението.
Решаването на уравнението чрез изграждането на неговата графика ще има формата на права линия, чиито точки са решение на полинома.

Видове системи от линейни уравнения

Най-простите примери са системите на линейни уравнения с две променливи X и Y.

F1 (x, y) = 0 и F2 (x, y) = 0, където F1,2 са функции и (x, y) са функционални променливи.

Решете системата от уравнения - това означава намиране на стойностите (x, y), при които системата се превръща в правилно равенство или установява, че няма подходящи стойности х и у.

Двойствени стойности (x, y), написани под формата на координатите на точка, се наричат ​​решение на система от линейни уравнения.

Ако системите имат едно общо решение или решения не съществуват, те се наричат ​​еквивалентни.

Хомогенните системи на линейни уравнения са системи, чиято дясна страна е равна на нула. Ако правото след знака на частта "равенство" има стойност или се изразява чрез функция, такава система не е хомогенна.

Броят на променливите може да бъде много по-голям от два, тогава трябва да говорим за пример за система от линейни уравнения с три променливи или повече.

Изправени пред системите на учениците,че броят на уравненията задължително трябва да съвпада с броя на неизвестните, но това не е така. Броят уравнения в системата не зависи от променливите, може да има толкова, колкото им харесва.

Обикновени и сложни методи за решаване на системи от уравнения

Няма общ аналитичен методрешения на такива системи, всички методи се основават на цифрови решения. В учебния курс по математика са описани подробно методи като пермутация, алгебрично добавяне, заместване, както и графичен и матричен метод, решение на Гаус.

Основната задача в преподаването на методи за решаване -това е да ви науча как правилно да анализирате системата и да намерите алгоритъма за оптимално решение за всеки пример. Основното нещо е да не се запомнят системата от правила и действия за всеки метод, а да се разберат принципите за прилагане на този или този метод

Решаване на примери на системи от линейни уравнения 7Класът на програмата за общо училище е съвсем прост и е обяснен подробно. Във всяка математика на учебника се отделя достатъчно внимание на този раздел. Решението на примери на системи от линейни уравнения по метода на Гаус и Крамер е разгледано по-подробно в първите курсове на висшите учебни заведения.

Решаване на системи чрез замяна

Действията на метода на заместване са насочени къмизразяване на стойността на една променлива през втората. Изразът се замества в оставащото уравнение, след това се довежда до формата с една променлива. Действието се повтаря в зависимост от броя неизвестни в системата

Даваме решение на пример за система от линейни уравнения от 7-ми клас чрез метода на заместване:

Както можете да видите от примера, променливата x беше изразеначрез F (X) = 7 + Y. Получената експресия, заместена във второто уравнение на системата на мястото на X, помага да се получи една променлива Y във второто уравнение. Решението на този пример не причинява трудности и ви позволява да получите стойността на Y. Последната стъпка е да проверите получените стойности.

Решете пример за система от линейни уравнениязаместването не винаги е възможно. Уравненията могат да бъдат сложни и изразяването на променливата чрез второто неизвестно ще се окаже твърде тромаво за по-нататъшни изчисления. Когато има повече от 3 непознати в системата, заместването също не е препоръчително.

Решение на пример за система от линейни нехомогенни уравнения:

Решение чрез алгебрично добавяне

Когато се търси решение на системите чрез метода на добавяне, се извършват условно добавяне и умножаване на уравнения с различни числа. Крайната цел на математическите действия е уравнение с една променлива.

За приложенията на този метод е необходима практикаи наблюдение. Решаването на системата от линейни уравнения чрез метода за добавяне на няколко променливи от 3 или повече не е лесно. Алгебричното добавяне е удобно, когато фракциите и десетичните знаци присъстват в уравненията.

Алгоритъм на решението:

1. Умножете двете страни на уравнението с определено число. В резултат на аритметичната операция един от коефициентите за променливата трябва да стане равен на 1.
2. Накрая добавете резултантния израз и намерете един от неизвестните.
3. Заменете тази стойност във второто уравнение на системата, за да намерите останалата променлива.

Методът за решаване чрез въвеждане на нова променлива

Нова променлива може да бъде въведена, ако в системата е необходимо да се намери решение за не повече от две уравнения, броят неизвестни трябва да бъде не повече от две.

Методът се използва за опростяване на един отуравнения, като въведете нова променлива. Новото уравнение се решава по отношение на неизвестното и получената стойност се използва за определяне на началната променлива.

От примера се вижда, че чрез въвеждане на нова променлива t, е възможно да се намали първото уравнение на системата до стандартната квадратична триномия. Решете полинома, като откриете дискриминацията.

Необходимо е да се намери стойността на дискриминатора чрезизвестна формула: D = b2 - 4 * a * c, където D е желаният дискриминатор, b, a, c са полиномните множители. В дадения пример, a = 1, b = 16, c = 39, следователно D = 100. Ако дискриминантата е по-голяма от нула, тогава двата разтвора: т = Ь ± √D / 2 * а, ако дискриминантата е по-малка от нула, тогава един разтвор: х = Ь / 2 * а.

Решението за получените системи се установява чрез метода на добавяне.

Визуален метод за решаване на системи

Подходящ за системи с 3 уравнения. Методът се състои в изчертаване на координатната ос на графиките на всяко уравнение, влизащо в системата. Координатите на точките на пресичане на кривите u ще бъдат общо решение на системата.

Графичният метод има редица нюанси. Нека разгледаме няколко вида решения за решаване на линейни уравнения по визуален начин.

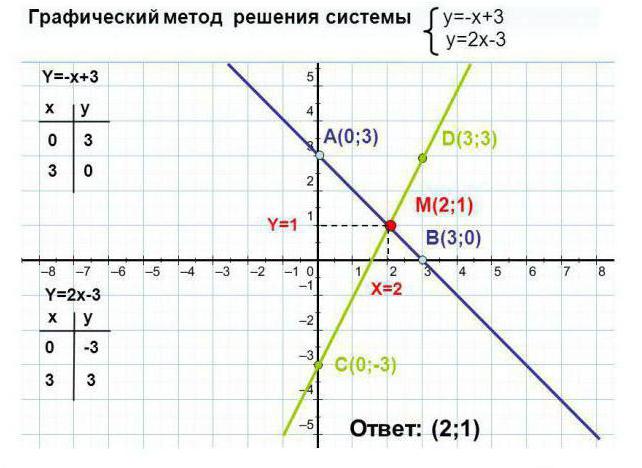
Както може да се види от примера, за всяка права линияконструирани две точки, стойностите на променливите х са избрани произволно: 0 и 3. На базата на стойностите на х, намерени стойностите за Y: 3 и 0 точки с координати (0, 3) и (3, 0) са маркирани в графиката и свързан с линия ,

Действието трябва да бъде повторено за второто уравнение. Точката на пресичане на линиите е решение на системата.

В следващия пример трябва да намерим графично решение на системата от линейни уравнения: 0.5x-y + 2 = 0 и 0.5x-y-1 = 0.

Както можете да видите от примера, системата няма решение, защото графиките са успоредни и не се пресичат по дължината им.

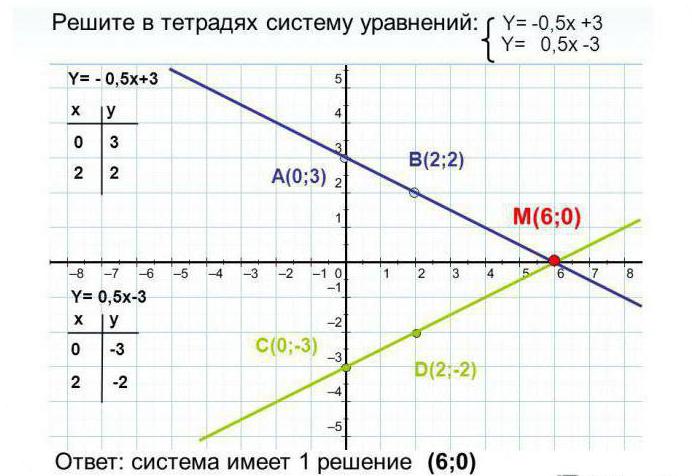
Системите от примери 2 и 3 са подобни, но сстава ясно, че техните решения са различни. Трябва да се помни, че не винаги е възможно да се каже дали системата има решение или не, винаги е необходимо да се създаде график.

Матрицата и нейните варианти

Матриците се използват за кратко записване на система от линейни уравнения. Матрицата се нарича таблица от специален вид, изпълнена с числа. Матрицата с формата n * m има n-редове и m-колони.

Матрицата е квадратна, когато е числотоколоните и редовете са равни една на друга. Матричният вектор е матрица на една колона с безкраен брой редове. Матрицата с тези на един от диагоналите и други нулеви елементи се нарича единица матрица.

Обратната матрица е такава матрица, умножена, с която оригиналната матрица се превръща в единична матрица, такава матрица съществува само за оригиналната квадратна матрица.

Правилата за трансформиране на система от уравнения в матрица

По отношение на системите на уравнения, коефициентите и свободните термини на уравненията са написани като номерата на матрицата, едно уравнение е един ред на матрицата.

Ред на матрицата се казва, че не е нула, ако понеедин елемент от низа не е нула. Следователно, ако в някое от уравненията броят на променливите е различен, тогава е необходимо да напишете нула на мястото на липсващото неизвестно.

Матричните колони трябва да съответстват стриктнопроменливи. Това означава, че коефициентите на променливата x могат да бъдат записани само в една колона, например първата, коефициентът на непознатото y е само във втората колона.

Когато матрицата се умножи, всички елементи на матрицата се умножават последователно с число.

Вариантите за намиране на обратната матрица

Формулата за намиране на обратната матрица е съвсем проста: K^-1= 1 / | K |, където K^-1 е обратната на матрицата и | K | матричен детерминант. К | не трябва да бъде нула, тогава системата има решение.

Детерминанта се изчислява лесно за матрица две по две, е необходимо само да се умножат диагонално елементите. За варианта "три по три", формулата | K | = a₁б₂в₃ + а₁б₃в₂ + а₃б₁в_{2 +} а₂б₃в₁ + а₂б₁в₃ + а₃б₂в₁, Можете да използвате формулата и можетене забравяйте, че трябва да вземете един елемент от всеки ред и всяка колона, така че продуктът да не повтаря колоната и номера на реда на елементите.

Решение на примери за системи от линейни уравнения по матричен метод

Матричният метод за търсене на решение прави възможно намаляването на тромавите записи при решаване на системи с голям брой променливи и уравнения.

В примера a_нм - коефициенти на уравнения, матрица - вектор x_п - променливи и б_п - безплатни членове.

След това трябва да намерим обратната матрица и да я умножим по оригиналната матрица. Намирането на стойностите на променливите в резултатната матрица на единиците е лесно изпълнима задача.

Решения на системите по Gauss метод

Във висшата математика се изследва Gauss методътзаедно с метода Cramer, и процесът на намиране на решения за системи се нарича Gauss-Cramer разтвор метод. Тези методи се използват при намирането на променливи системи с голям брой линейни уравнения.

Гаусовият метод е много подобен на използваните решениязамествания и алгебрични добавки, но по-систематични. В учебния курс, Gauss методът се използва за системи от 3 и 4 уравнения. Целта на метода е да доведе системата до формата на обърнат трапец. С помощта на алгебрични трансформации и замествания, стойността на една променлива се намира в едно от уравненията на системата. Второто уравнение е израз с 2 неизвестни, добре, 3 и 4 - съответно, с 3 и 4 променливи.

След редуциране на системата до описаната форма, по-нататъшното решение се свежда до последователно заместване на известни променливи в уравненията на системата.

В училищните учебници за степен 7, пример за решение по Gauss метод е описан, както следва:

Както може да се види от примера, в стъпка (3) две уравнения 3х₃-2x₄= 11 и 3х₃+ 2x₄= 7. Решението на всяко от уравненията ще даде възможност да се знае една от променливите x_п.

Теорема 5, който е споменат в текста, гласи, че ако едно от уравненията на системата е заменено с една еквивалентна, тогава получената система също ще бъде еквивалентна на оригиналната.

Гауският метод е трудно за възприемане от страна на ученицитегимназията, но той е един от най-интересните начини да се развиват децата остроумие, записани в по-задълбочено проучване на програмата по математика и часовете по физика.

За простота е обичайно да напишете изчисления, както следва:

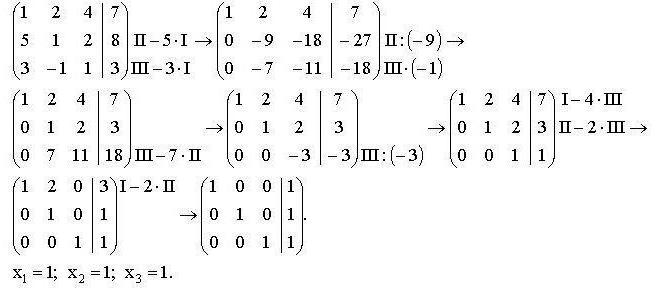
Коефициентите на уравненията и свободните терминиса написани под формата на матрица, където всеки ред на матрицата съответства на едно от уравненията на системата. Вертикалната линия разделя лявата страна на уравнението отдясно. Римските цифри обозначават броя на уравненията в системата.

Първо, напишете матрицата от кояторабота, след това всички действия, извършени с една от линиите. Получената матрица е написана след знака "стрелка" и продължава да изпълнява необходимите алгебрични действия, докато резултатът не бъде постигнат.

В резултат на това трябва да се получи матрица, в коятоедин от диагоналите е 1, а всички останали коефициенти са нула, т.е. матрицата се намалява до единична форма. Не трябва да забравяме да правим изчисления с цифрите и на двете страни на уравнението.

Този метод на записване е по-малко тромав и позволява да не се разсейва чрез изброяване на многобройни непознати.

Безплатно използване на всеки метод за разтварянеще изисква внимание и известен опит. Не всички методи имат приложен характер. Някои от начините за намиране на решения са по-предпочитани в друга област на човешката дейност, докато други съществуват за целите на обучението.